위치 에너지

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 종류
4. 위치 에너지와 힘
5. 일과 위치 에너지
6. 힘점에 의한 운동 (천문학 및 미시물리학)
참조

1. 개요

위치 에너지는 물리학에서 물체의 위치에 따라 결정되는 에너지의 한 형태이다. 19세기 스코틀랜드 물리학자 윌리엄 랭킨이 처음 사용했으며, 중력, 탄성, 전기력 등 다양한 힘과 관련된다. 중력 위치 에너지는 물체를 들어 올리는 데 필요한 일과 관련되며, 탄성 위치 에너지는 변형된 물체가 원래 형태로 돌아가려는 힘에 의해 저장된다. 정전기적 위치 에너지는 전하를 띤 물체의 상대적 위치에 따라 결정되며, 화학 위치 에너지는 분자 구조와 관련된다. 위치 에너지는 힘과 밀접하게 관련되어 있으며, 힘이 경로에 의존하지 않는 경우 스칼라 퍼텐셜 장을 정의하고 힘은 퍼텐셜 장의 기울기의 음수로 표현될 수 있다. 천문학 및 미시물리학에서는 무한 원점을 위치 에너지의 기준면으로 삼아 에너지를 기술한다.

더 읽어볼만한 페이지

에너지의 유형 - 열에너지
열에너지는 열역학에서 뜨거운 계에서 차가운 계로 자발적으로 전달되는 에너지 형태를 의미하며, 내부 에너지와 관련되지만 상전이 등 복잡한 계에서는 명확하게 정의되지 않고, 다양한 형태로 나타날 수 있으며, 열 흐름 밀도와 관련된 에너지에도 적용된다.
에너지의 유형 - 복사 에너지
복사 에너지는 발생원에서 자유 공간으로 이동하는 에너지의 한 형태로, 전자기파, 음파, 중력파, 물질파 등을 포함하며 다양한 분야에서 활용되고 개방계로 에너지가 출입하는 주요 메커니즘 중 하나이다.
퍼텐셜 - 전위
전위는 전기장 내 단위 전하의 위치 에너지로, 정전기학에서는 기준점에 따라 정의되며 전위차만이 의미를 갖고, 전기장의 음의 기울기로 표현되고, 전기 공학에서는 회로 해석에 활용된다.
퍼텐셜 - 리에나르-비헤르트 퍼텐셜
리에나르-비헤르트 퍼텐셜은 운동하는 점전하가 속도와 가속도를 고려하여 생성하는 전자기 퍼텐셜을 기술하는 공식으로, 전자기 복사 효과를 포함하여 전자기장을 정확하게 계산하고 고전 전자기학과 상대성이론 발전에 기여했으나 양자역학적 영역에서는 한계를 보인다.
중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다.
중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.

위치 에너지
단위	줄 (J)
유도	U = m ⋅ g ⋅ h (중력)
설명

2. 역사

"위치 에너지"라는 용어는 19세기에 스코틀랜드의 물리학자인 윌리엄 랭킨이 처음 사용하였다.^[24] 1840년경부터 과학자들은 에너지와 일을 정의하고 이해하려고 노력했다.^[4] 1853년 스코틀랜드의 엔지니어이자 물리학자인 윌리엄 랭킨은 "퍼텐셜 에너지"라는 용어를 만들었는데, 이는 아리스토텔레스의 연구로 거슬러 올라가는 "실제" 대 "잠재적"이라는 쌍의 일부로 선택한 것이다.^[5] 1867년 랭킨은 같은 주제에 대한 논의에서 퍼텐셜 에너지를 '구성 에너지'로, 실제 에너지를 '활동 에너지'와 대조적으로 설명했다. 또한 같은 해 윌리엄 톰슨은 "퍼텐셜 에너지"의 반대말로 "운동 에너지"를 도입하여 모든 실제 에너지는 1/2mv²의 형태를 취한다고 주장했다. 이 가설이 널리 받아들여지면서 "실제 에너지"라는 용어는 점차 사라졌다.^[6]

3. 종류

위치 에너지에는 다양한 종류가 있으며, 각각 특정한 힘과 관련되어 있다.

위치 에너지의 종류
종류	관련 힘	설명
탄성 위치 에너지	탄성력	용수철과 같이 탄성을 가진 물체가 변형될 때 저장되는 에너지
중력 위치 에너지	중력	물체가 지구의 중력에 대항하여 들어 올려질 때 저장되는 에너지
전기 위치 에너지	쿨롱 힘	전하를 띤 물체가 다른 전하를 띤 물체에 대한 상대적 위치 때문에 가지는 에너지
핵 위치 에너지	강한 핵력, 약한 핵력	원자핵 내부 소립자들의 위치 에너지
분자간 위치 에너지	분자간 힘	분자 간의 상대적 위치에 따라 저장되는 에너지
화학 위치 에너지	쿨롱 힘	원자 또는 분자의 구조적 배열과 관련된 에너지, 화석 연료 등에 저장

열에너지는 입자의 무작위 운동의 운동 에너지와 그 배열의 위치 에너지, 두 가지 구성 요소를 갖는다.

3. 1. 중력 위치 에너지

중력 위치 에너지는 중력과 관련된 위치 에너지로, 물체를 지구의 중력에 대항하여 들어 올리는 데 일이 필요하기 때문에 생기는 에너지이다. 높은 위치 때문에 생기는 위치 에너지를 중력 위치 에너지라고 하며, 높은 곳에 있는 저수지의 물이나 댐 뒤에 가두어진 물에서 볼 수 있다. 만약 어떤 물체가 중력장 내의 한 점에서 다른 점으로 떨어진다면, 중력은 물체에 양의 일을 하고, 중력 위치 에너지는 같은 양만큼 감소한다.

책상 위에 놓인 책을 생각해 보자. 책을 바닥에서 책상까지 들어 올리면, 어떤 외부 힘이 중력에 대항하여 작용한다. 책이 바닥으로 다시 떨어지면, 책이 받는 "낙하" 에너지는 중력에 의해 제공된다. 따라서 책이 책상에서 떨어지면, 이 위치 에너지는 책의 질량을 가속시키는 데 사용되고 운동 에너지로 변환된다. 책이 바닥에 부딪히면 이 운동 에너지는 충격에 의해 열, 변형 및 소리로 변환된다.

물체의 중력 위치 에너지에 영향을 미치는 요인은 어떤 기준점에 대한 높이, 질량, 그리고 물체가 있는 중력장의 세기이다. 따라서 책상 위에 놓인 책은 더 높은 장롱 위에 놓인 같은 책보다 중력 위치 에너지가 적고, 같은 책상 위에 놓인 더 무거운 책보다 중력 위치 에너지가 적다. 달 표면 위의 특정 높이에 있는 물체는 지구 표면 위의 같은 높이에 있는 물체보다 중력 위치 에너지가 적다. 달의 중력이 더 약하기 때문이다.

중력장의 세기는 위치에 따라 변한다. 그러나 중력장의 근원 중심으로부터의 거리에 비해 거리 변화가 작을 경우, 이러한 장 세기의 변화는 무시할 만하고 특정 물체에 작용하는 중력은 일정하다고 가정할 수 있다. 예를 들어 지구 표면 근처에서는 중력 가속도가 일정한 (표준중력)라고 가정한다. 이 경우, 일에 대한 방정식과 다음 방정식을 사용하여 중력 위치 에너지에 대한 간단한 식을 유도할 수 있다.

:

W_F = -\Delta U_F.

높이 올려진 물체가 가지는 중력 위치 에너지의 양은 그것을 들어올리는 데 필요한 일과 같다. 이 일은 물체를 위로 이동시키는 데 필요한 힘에 수직으로 이동한 거리를 곱한 것과 같다 ( 참조). 일정한 속도로 움직일 때 필요한 위쪽 힘은 물체의 무게 와 같으므로, 높이 만큼 들어올리는 데 필요한 일은 의 곱이다. 따라서 질량, 중력, 고도만을 고려할 때 방정식은 다음과 같다.^[9]

:

U = mgh

여기서 는 지구 표면에 있는 물체에 대한 위치 에너지, 는 물체의 질량, 는 중력 가속도, 그리고 ''h''는 물체의 고도이다.^[10]

따라서 위치 에너지 차이는 다음과 같다.

:

\Delta U = mg \Delta h.

그러나 거리의 변화가 클 경우 가 일정하다는 근사는 더 이상 유효하지 않으며, 중력 퍼텐셜 에너지를 결정하기 위해 미적분학과 일의 일반적인 수학적 정의를 사용해야 한다. 퍼텐셜 에너지를 계산하기 위해, 크기가 뉴턴의 만유인력의 법칙에 의해 주어지는 중력을 두 물체 사이의 거리 에 대해 적분할 수 있다. 그 정의를 사용하면, 뉴턴의 중력 상수 를 사용하여 거리 에 있는 과 질량계의 중력 퍼텐셜 에너지는 다음과 같다.

:

U = -G \frac{m_1 M_2}{r} + K,

여기서 는 퍼텐셜을 측정하는 기준점의 선택에 따라 달라지는 임의의 상수이다. (즉, 무한대의 점에 대한 상대적 값)이라는 규칙을 선택하면 계산이 간단해지지만, 를 음수로 만드는 단점이 있다.

에 대한 이 공식을 고려하면, 개의 물체계의 총 퍼텐셜 에너지는 두 물체의 모든

\frac{n ( n - 1 )}{2}

쌍에 대해 해당 두 물체계의 퍼텐셜 에너지를 합산하여 구한다.

물체계를 물체를 구성하는 작은 입자들의 결합된 집합으로 간주하고 이전 결과를 입자 수준에 적용하면 음의 중력 결합 에너지를 얻는다. 이 퍼텐셜 에너지는 각 물체의 음의 중력 결합 에너지를 포함하기 때문에 물체계의 총 퍼텐셜 에너지보다 더 강하게 음수이다. 물체계의 퍼텐셜 에너지는 물체들을 서로 무한히 멀리 분리하는 데 필요한 에너지의 음수인 반면, 중력 결합 에너지는 모든 입자들을 서로 무한히 멀리 분리하는 데 필요한 에너지이다.

:

U = - m \left(G \frac{ M_1}{r_1}+ G \frac{ M_2}{r_2}\right)

따라서,

:

U = - m  \sum G \frac{ M}{r} ,

모든 퍼텐셜 에너지와 마찬가지로, 대부분의 물리적 목적을 위해서는 중력 퍼텐셜 에너지의 차이만 중요하며, 영점의 선택은 임의적이다. 하나의 특정한 유한한 ''r''을 다른 것보다 선호할 만한 합리적인 기준이 없다는 점을 고려할 때, 가 0이 되는 거리에 대해 합리적인 선택은 두 가지뿐이다.

r = 0

과

r = \infty

이다. 무한대에서

U = 0

으로 선택하는 것이 특이하게 보일 수 있으며, 중력 에너지가 항상 음수라는 결과는 반직관적으로 보일 수 있지만, 이 선택을 통해 중력 퍼텐셜 에너지 값을 유한하게(비록 음수이지만) 만들 수 있다.

손으로 공을 들어 올려서 천천히 놓는 경우를 생각해 보자. 공은 중력에 따라 아래로 떨어진다.

이때 공이 가지는 에너지에 주목하자. 공을 들어 올렸을 때, 그 공은 '''위치 에너지'''를 얻었다고 생각한다. 얻은 에너지의 크기는 공을 들어 올리는 데 필요한 에너지와 같다. 그리고 공을 지탱하던 손이 놓인 순간, 위치 에너지는 운동 에너지로 변하기 시작한다. 운동 에너지란 물체가 움직이고 있을 때 가지는 에너지이다. 공이 떨어짐에 따라 위치 에너지는 감소하고, 대신 운동 에너지는 증가한다. 위치 에너지 + 운동 에너지, 즉 물체가 가지는 모든 에너지를 역학적 에너지라고 한다.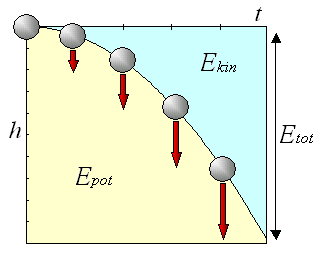

그림은 낙하하는 물체의 에너지 변화를 나타낸다. ''h''는 물체의 높이, ''t''는 시간, ''E_pot''는 위치 에너지, ''E_kin''는 운동 에너지, ''E_tot''는 역학적 에너지이다. 물체의 낙하에 따라 위치 에너지(노란 부분)는 감소하고, 운동 에너지(파란 부분)는 증가한다.

여기서 중요한 것은 공이 낙하하는 동안 역학적 에너지는 항상 일정하게 변하지 않는다는 것이다. 물체가 움직일 때는 에너지의 종류는 변하지만 그 총량은 증가하거나 감소하지 않는다. 이 법칙을 역학적 에너지 보존 법칙이라고 한다. 운동 에너지를 ''K'', 위치 에너지를 ''U'', 역학적 에너지를 ''E''라고 하면, ''K＋U＝E''로 나타낼 수 있다. 이것은 뉴턴 역학 3법칙으로부터 유도할 수 있다.

지표 부근에서 질량이 *m*인 물체가 기준면으로부터 *h*만큼 높은 위치에 있다고 하자. 그 물체가 가지는 위치 에너지는 중력가속도를 상수 *-g*로 하면

:

\left\lbrace f = -mg\right\rbrace \longrightarrow U(h) = -\int_0^h (-mg) dr = mgh

로 표현된다.

위 식은 만유인력에 의한 위치 에너지의 지표 부근에서의 근사식이다. 만유인력의 위치 에너지 U는 지구의 질량을 *M*, 만유인력 상수를 *G*로 하면, 지구 중심으로부터 거리 *r*만큼 떨어진 질량 *m*의 물체에 대해

:

\left\lbrace f(r) = -G\frac{Mm}{r^2}\right\rbrace \longrightarrow U(r) = -\int \left(-G\frac{Mm}{r^2}\right)\,dr = -G\frac{Mm}{r} + C.

단, 위치 에너지의 기준점은 (적분 상수 *C*로서) 임의로 정할 수 있지만, 일반적으로는 만유인력이 0이 되는 무한원점을 기준으로 한다.

이제, 지표로부터 *h*만큼 높은 질량 *m*의 물체의 위치 에너지를 생각하자. 지구 중심으로부터 지표까지의 거리를 *R*로 하면, 지구 중심으로부터 물체까지의 거리는 *R*+*h*가 된다. 위 식에 대입하면,

:

U = -G\frac{Mm}{R+h}

가 된다. 지표를 기준으로 하기 위해 지표에서의 위치 에너지를 빼면,

:

E = -G\frac{Mm}{R+h} - \left(-G\frac{Mm}{R}\right)

제1항을 테일러 전개하고, 2차 이상의 식은 작으므로 0으로 보고 생략하면

:

E = -G\frac{Mm}{R} + G\frac{Mm}{R^2}h - \left(-G\frac{Mm}{R}\right)

이 되고, 제2항의

:

G\frac{M}{R^2} = G\frac{Mm}{R^2}\frac{1}{m} = \frac{F}{m} = g

　(F는 지표의 물체에 작용하는 힘)

는 지표 부근의 중력가속도 *g*이므로 대입하면,

:

\mathbf{}E = mgh

가 된다.

3. 1. 1. 중력 위치 에너지의 활용

트레뷰셋은 추의 중력 위치 에너지를 이용하여 이상의 거리에 발사체를 발사한다.

중력 위치 에너지는 여러 실용적인 용도로 사용된다. 특히 양수 발전의 발전에 사용된다. 예를 들어, 웨일스의 디노르위그(Dinorwig)에는 높이가 다른 두 개의 호수가 있다. 전력이 과잉 공급되어 필요하지 않을 때 (따라서 비교적 저렴할 때)에는 물을 높은 호수로 퍼 올려 전기에너지를 (펌프 작동) 중력 위치 에너지로 변환한다. 전력 수요가 최고조에 달하는 시간에는 물이 발전기 터빈을 통해 아래로 흘러내리면서 위치 에너지를 운동 에너지로, 다시 전기에너지로 변환한다. 이 과정은 완벽하게 효율적이지 않으며, 과잉 전력의 원래 에너지 중 일부는 마찰로 손실된다.^[12]^[13]^[14]^[15]^[16]

중력 위치 에너지는 낙하하는 추가 장치를 작동시키는 시계, 반중량을 사용하여 엘리베이터, 크레인 또는 창문을 들어 올리는 데에도 사용된다. 롤러코스터는 위치 에너지를 활용하는 재미있는 방법이다. 체인을 사용하여 차량을 경사면으로 이동시켜(중력 위치 에너지를 축적) 그 에너지를 낙하하면서 운동 에너지로 변환한다.

또한 자동차, 트럭, 기차, 자전거, 비행기 또는 파이프라인 내의 유체와 같이 수송에서 중력 위치 에너지를 이용하여 내리막길을 내려가는(어쩌면 활강하는) 데 사용된다. 경우에 따라 내리막의 위치 에너지에서 얻은 운동 에너지를 사용하여 다음 경사면을 오르기 시작할 수 있는데, 도로가 굴곡이 있고 잦은 경사가 있는 경우에 발생한다. 미국에서는 고도로 올려진 철도 차량의 형태로 저장된 에너지를 필요에 따라 전력망에 전력으로 변환하는 시스템인 첨단 철도 에너지 저장(ARES)이 상용화되고 있다.^[17]^[18]^[19]

물의 위치 에너지는 베르누이 정리에 따라 수력으로 이용된다.

3. 2. 탄성 위치 에너지

탄성 위치 에너지는 용수철과 같이 탄성을 가진 물체가 변형될 때 저장되는 위치 에너지이다. 복원력(Restoring force)이 작용할 때 위치 에너지가 존재하는데, 용수철이 늘어나면 원래 형태로 돌아가려는 탄성력이 작용하는 것이 그 예시이다.^[1]

위치 에너지는 상대적인 위치에 따라 물체가 가지는 에너지 간의 차이를 의미하며, 기준점이나 기준면을 정해서 사용한다.^[1]

예를 들어, 손으로 공을 들어 올려서 천천히 놓는 경우, 공은 중력에 따라 아래로 떨어진다. 공을 들어 올렸을 때, 그 공은 위치 에너지를 얻게 되며, 이 위치 에너지는 공을 들어 올리는 데 필요한 에너지와 같다. 공을 놓으면 위치 에너지는 운동 에너지로 변환되기 시작한다. 공이 떨어짐에 따라 위치 에너지는 감소하고 운동 에너지는 증가한다. 이때, 위치 에너지와 운동 에너지의 합, 즉 역학적 에너지는 일정하게 유지된다. 이를 역학적 에너지 보존 법칙이라고 한다.^[1]

수평 용수철은 축 방향 변형에 비례하는 힘( )을 작용한다. 이 용수철이 하는 일은 다음과 같이 계산될 수 있다.^[1]

:

W = \int_0^t\mathbf{F}\cdot\mathbf{v}\,dt= -\int_0^t kx v_x \, dt=-\int_0^t k x \frac{dx}{dt}dt= \int_{x(t_0)}^{x(t)} k x \, dx= \frac{1}{2} kx^2

여기서 함수

U(x) = \frac{1}{2}kx^2,

는 선형 용수철의 위치 에너지를 나타낸다.^[1]

3. 2. 1. 탄성 위치 에너지의 활용

양궁은 인류가 탄성 위치 에너지를 활용한 가장 오래된 예시 중 하나이다.

탄성 위치 에너지는 탄성을 가진 물체가 장력이나 압축력을 받아 변형되었을 때 저장되는 위치 에너지이다. 예를 들어 활이나 투석기와 같은 물체가 변형될 때 에너지가 저장된다. 이 에너지는 물체를 구성하는 원자와 분자 사이의 힘, 주로 전자기력이 물체를 원래 모양으로 되돌리려고 할 때 발생한다. 물체가 원래 형태로 돌아오면, 저장되었던 탄성 위치 에너지는 운동 에너지로 변환된다.

용수철의 경우, 기준 위치(보통 자연장)에서 ''x''만큼 벗어난 위치에 있을 때, 용수철 상수를 ''k''라고 하면, 물체가 가지는 위치 에너지(탄성 에너지)는 다음과 같이 표현된다.

:

\left\lbrace f(x)=-k x\right\rbrace \longrightarrow E = -\int_{0}^{x}\left(-kx\right)dx =\frac{1}{2}kx^2

이 식은 훅의 법칙을 통해 유도될 수 있다. 여기서 물체를 자유롭게 하면 물체는 단진동을 시작한다. 하지만 실제로는 용수철의 늘어남과 힘의 크기가 정확하게 비례하지 않기 때문에, 이 식은 ''x''가 비교적 작은 경우에만 성립한다.

3. 3. 전기적 위치 에너지

전하를 띤 물체는 그 전하와 관련된 여러 힘에 의해 위치 에너지를 가질 수 있다. 이러한 종류의 위치 에너지는 크게 정전기 위치 에너지와 전자기 위치 에너지(때로는 자기 위치 에너지라고도 함) 두 가지로 나뉜다.

두 물체 사이의 정전기적 위치 에너지는 전하 ''Q''가 다른 전하 ''q''에 작용하는 힘으로부터 얻어진다.

:

\mathbf{F}_{e} = -\frac{1}{4\pi\varepsilon_0} \frac{Qq}{r^2} \mathbf{\hat{r}},

여기서

\mathbf{\hat{r}}

은 ''Q''에서 ''q''를 가리키는 길이 1의 벡터이고, ''ε''₀는 진공 유전율이다.

어떤 물체의 전하가 정지 상태로 가정될 수 있다면, 다른 대전된 물체에 대한 상대적 위치 때문에 위치 에너지를 갖는다. 정전기적 위치 에너지는 전기장 내에 있는 정지 상태의 대전 입자의 에너지이다. 이는 무한히 먼 거리에서 현재 위치로 옮기는 데 필요한 일로 정의되며, 물체에 작용하는 비전기적 힘에 대한 보정이 적용된다. 이 에너지는 일반적으로 근처에 다른 대전된 물체가 있으면 0이 아니다.

정전기력장에서 ''q''를 ''A''에서 임의의 점 ''B''로 옮기는 데 필요한 일 ''W''는 다음과 같이 주어진다.

:

\Delta U_{AB}({\mathbf{r}})=-\int_{A}^{B} \mathbf{F_e} \cdot d\mathbf{r}

일반적으로 줄(J) 단위로 표시된다. '전위'(일반적으로 전압을 나타내는 ''V''로 표시됨)라고 하는 관련된 양은 단위 전하당 전기 위치 에너지와 같다.

외부에서 생성된 자기 B장 내의 자기 모멘트

\boldsymbol{\mu}

의 에너지는 다음과 같은 위치 에너지를 갖는다.^[20]

:

U=-\boldsymbol{\mu}\cdot\mathbf{B}.

자기장 내의 자화 은 다음과 같다.

:

U = -\frac{1}{2}\int \mathbf{M}\cdot\mathbf{B} \, dV,

여기서 적분은 모든 공간에 걸쳐 수행될 수 있으며, 또는 동등하게 이 0이 아닌 곳에서 수행될 수 있다.^[21]

자기 위치 에너지는 자성체 사이의 거리뿐만 아니라 자기장 내에서 그 물질의 방향 또는 정렬과도 관련된 에너지 형태이다. 예를 들어, 나침반 바늘은 지구 자기장의 남극과 북극에 정렬될 때 자기 위치 에너지가 가장 낮다. 외부 힘에 의해 바늘이 움직이면 지구 자기장에 의해 바늘의 자기 쌍극자에 토크가 작용하여 다시 정렬되도록 한다. 바늘의 자기 위치 에너지는 바늘의 자기장이 지구 자기장과 같은 방향일 때 가장 높다. 두 개의 자석은 서로 및 그 사이의 거리에 따라 위치 에너지를 갖지만, 이는 또한 그들의 방향에도 의존한다. 반대 극을 떼어 놓으면 위치 에너지는 거리가 멀수록 높아지고 가까울수록 낮아진다. 반대로, 같은 극은 함께 밀착되었을 때 위치 에너지가 가장 높고, 서로 멀어졌을 때 가장 낮다.^[22]^[23]

3. 3. 1. 전기적 위치 에너지의 활용

전하를 띤 물체는 전하와 관련된 힘 때문에 위치 에너지를 가질 수 있다. 이러한 위치 에너지는 정전기 위치 에너지와 전자기 위치 에너지(또는 자기 위치 에너지) 두 가지로 나뉜다.

어떤 물체의 전하가 정지 상태라고 가정하면, 다른 대전된 물체에 대한 상대적 위치 때문에 위치 에너지를 갖는다. 정전기적 위치 에너지는 전기장 안에 있는 정지 상태의 대전 입자가 가지는 에너지이다. 이 에너지는 무한히 먼 거리에서 현재 위치로 옮기는 데 필요한 일로 정의되며, 물체에 작용하는 비전기적 힘에 대한 보정이 적용된다. 이 에너지는 일반적으로 근처에 다른 대전된 물체가 있으면 0이 아니다.

전기 위치 에너지와 관련된 물리량으로 '전위'(전압을 나타내는 ''V''로 표시)가 있으며, 단위 전하당 전기 위치 에너지와 같다.

전하 주위에는 정전 포텐셜 ''V''가 발생한다. 원점에 전하량 ''q' ''의 전하를 놓았을 때,

:

V=-\int_{\infty}^{r}\frac{q'}{4\pi\epsilon_0r^2}dr=\frac{1}{4\pi\epsilon_0}\frac{q'}{r}

가 된다. 또한 원점에서 거리 ''r''만큼 떨어진 지점에 전하량 ''q''의 다른 전하를 놓으면, 그 전하는 다음과 같은 위치 에너지를 갖는다.

:

U=qV=\frac{1}{4\pi\epsilon_0}\frac{qq'}{r}

여기서

\epsilon_0

는 진공의 유전율이다.

전하의 존재는 주위를 전기적으로 왜곡시켜 전장을 형성하고, 전하 변화에 따른 전기장의 변화가 광속으로 전달된다. 쿨롱의 힘은 이 전장에서 발생한다고 해석되며, 이 전장을 매개로 한 작용을 근접 상호 작용이라고 한다.

3. 4. 핵 위치 에너지

핵 위치 에너지(Nuclear potential energy^영어)는 원자핵 내부 소립자들의 위치 에너지이다. 핵입자들은 강한 핵력(strong nuclear force)에 의해 서로 결합되어 있으며, 약한 핵력(Weak nuclear force)은 베타 붕괴(beta decay)와 같은 특정 종류의 방사성 붕괴에 대한 위치 에너지를 제공한다.^[1]

핵입자인 양성자와 중성자는 핵분열과 핵융합 과정에서 파괴되지 않지만, 이들의 집합체는 개별적으로 자유롭게 존재할 때보다 질량이 적을 수 있다. 이 경우 이 질량 차이는 핵반응에서 열과 방사선으로 방출될 수 있다(열과 방사선은 누락된 질량을 가지고 있지만, 종종 측정되지 않는 시스템에서 빠져나간다). 태양의 에너지는 이러한 에너지 변환의 한 예로, 태양에서는 수소 핵융합 과정을 통해 매초 약 400만ton의 태양 물질이 전자기 에너지로 변환되어 우주로 방출된다.^[1]

3. 4. 1. 핵 위치 에너지의 활용

핵 위치 에너지는 원자핵 내부의 소립자들의 위치 에너지이다. 핵입자들은 강한 핵력에 의해 서로 결합되어 있다. 약한 핵력은 베타 붕괴와 같은 특정 종류의 방사성 붕괴에 대한 위치 에너지를 제공한다.^[1]

핵입자인 양성자와 중성자는 핵분열과 핵융합 과정에서 파괴되지 않지만, 이들의 집합체는 개별적으로 자유롭게 존재할 때보다 질량이 적을 수 있으며, 이 경우 이 질량 차이는 핵반응에서 열과 방사선으로 방출될 수 있다. 태양의 에너지는 이러한 에너지 변환의 한 예이다. 태양에서는 수소 핵융합 과정을 통해 매초 약 400만ton의 태양 물질이 전자기 에너지로 변환되어 우주로 방출된다.^[1]

3. 5. 분자간 위치 에너지

분자력에 대한 일은 분자 간 위치 에너지라고 한다.^[1] 화석 연료 따위에 저장된 에너지를 일컫는 화학 위치 에너지는 분자 내부의 재배열 과정 중에 전기력에 대해 한 일이 된다.^[1]

3. 6. 화학 위치 에너지

화학 위치 에너지는 원자 또는 분자의 구조적 배열과 관련된 위치 에너지의 한 형태이다. 이러한 배열은 분자 내의 화학 결합이나 다른 요인의 결과일 수 있다. 화학 물질의 화학 에너지는 화학 반응을 통해 다른 형태의 에너지로 변환될 수 있다. 예를 들어 연료가 연소될 때 화학 에너지는 열로 변환되며, 이는 생물체에서 음식물이 대사되는 것과 같은 경우이다. 녹색 식물은 광합성이라는 과정을 통해 태양 에너지를 화학 에너지로 변환하며, 전기 에너지는 전기화학 반응을 통해 화학 에너지로 변환될 수 있다.^[1]

화학 퍼텐셜은 화학 반응, 공간 이동, 저장소와의 입자 교환 등의 형태로 물질의 구성 변화 가능성을 나타내는 데 사용되는 유사한 용어이다.^[1]

3. 6. 1. 화학 위치 에너지의 활용

화학 위치 에너지는 원자나 분자가 구조적으로 어떻게 배열되어 있는지와 관련된 위치 에너지의 한 형태이다. 이러한 배열은 분자 내의 화학 결합이나 다른 요인 때문에 나타날 수 있다. 어떤 물질이 가진 화학 에너지는 화학 반응을 통해 다른 에너지 형태로 바뀔 수 있다. 예를 들어 연료가 탈 때 화학 에너지는 열로 바뀌는데, 이는 생물체에서 음식물이 소화되는 과정과 같다. 녹색 식물은 광합성을 통해 태양 에너지를 화학 에너지로 바꾸고, 전기 에너지는 전기화학 반응을 통해 화학 에너지로 바뀔 수 있다.

화학 퍼텐셜이라는 비슷한 용어는 화학 반응, 공간 이동, 저장소와의 입자 교환 등 물질의 구성이 바뀔 가능성을 나타내는 데 쓰인다.

4. 위치 에너지와 힘

위치 에너지는 계에 저장되는 에너지로, 복원력이 작용할 때 존재한다. 예를 들어, 용수철이 늘어나면 원래 형태로 돌아가려는 힘이 작용하고, 질량이 지면에서 들어 올려지면 아래 방향으로 중력이 작용한다. 이러한 상황에서 처음에 가해진 행동(질량을 들어 올리거나 용수철을 당기는 것)은 에너지를 필요로 한다. 이 에너지는 중력장 하의 물체의 위치나 용수철의 변형된 형태에 저장된다.^[7]

저장된 에너지는 용수철을 놓거나 질량을 떨어뜨렸을 때 복원력에 의해 운동 에너지로 바뀐다. 용수철의 경우 탄성력이, 질량의 경우 중력이 복원력으로 작용한다. 롤러코스터를 예로 들면, 롤러코스터가 경사를 올라갈 때 위치 에너지를 가지게 되며, 최고점에서 위치 에너지가 가장 크다. 롤러코스터가 내려가면서 위치 에너지는 운동 에너지로 바뀌고, 최저점에서 운동 에너지가 가장 크다. 마찰로 손실되는 에너지를 무시하면, 운동 에너지와 위치 에너지는 에너지 보존 법칙을 만족한다.^[7]

좀 더 엄밀하게 말하면, 위치 에너지는 상대적인 위치에 따라 물체가 가지는 에너지 간의 차이를 의미한다. 그렇지 않은 경우는 기준점이나 기준면을 정해서 사용한다.

위치 에너지에는 다양한 종류가 있으며, 각각의 위치 에너지에는 각각의 힘이 대응한다. 예를 들어 탄성력에 의한 것은 탄성 위치 에너지, 중력에 의한 것은 중력 위치 에너지, 전기력에 의한 것은 전기 위치 에너지라고 불린다.

위치 에너지에서 유도할 수 있는 힘은 보존력이라고도 부르며, 보존력이 한 일은 다음과 같이 나타낼 수 있다.

: $\,W = -\Delta U$

여기서 $\Delta U$ 는 위치 에너지의 변화를 의미한다. 마이너스 기호는 역장과 반대 방향으로 행해진 일이 위치 에너지를 증가시켰음을 의미하며, 역장에 의한 일은 위치 에너지를 감소시킨다. 일반적으로 위치 에너지를 나타내는 기호로 ''U'', ''V'', ''E_p''를 사용한다.^[7]

퍼텐셜 에너지는 힘과 밀접하게 관련되어 있다. 물체가 A에서 B로 이동할 때 힘이 한 일이 경로에 의존하지 않는다면(보존력에 의해 일이 행해진다면), A에서 측정한 이 힘의 일은 공간의 다른 모든 점에 스칼라 값을 할당하고 스칼라 퍼텐셜장을 정의한다. 이 경우 힘은 퍼텐셜 장의 벡터 기울기의 음수로 정의될 수 있다.^[7]

힘이 움직이는 물체에 작용할 때, 일의 적분이 경로에 무관하다면 그 일은 퍼텐셜 에너지의 변화를 나타낸다. 힘 '''F'''와 그 작용점의 속도 '''v'''의 스칼라 곱은 특정 시간에 시스템에 입력되는 일률을 정의한다. 이 일률을 작용점의 궤적 ''d''='''x'''(t)에 대해 적분하면 힘에 의해 시스템에 입력된 일을 정의한다.

적용된 힘에 대한 일이 경로에 무관하다면, 힘이 한 일은 작용점의 궤적의 시작과 끝에서 평가된다. 즉, "퍼텐셜"이라고 하는 함수 ''U''('''x''')가 있으며, 이 함수는 두 점 '''x'''_A와 '''x'''_B에서 평가하여 이 두 점 사이의 임의의 궤적에 대한 일을 얻을 수 있다. 양의 일이 퍼텐셜의 감소가 되도록 이 함수를 음수 부호로 정의하는 것이 관례이며, 다음과 같다.

: $W =\int_{C} \mathbf{F} \cdot d\mathbf{x} = U(\mathbf{x}_\text{A})-U(\mathbf{x}_\text{B})$

여기서 ''C''는 A에서 B로 이동하는 궤적이다. 일이 경로에 무관하기 때문에, 이 식은 A에서 B로 가는 임의의 궤적 ''C''에 대해 성립한다.

함수 ''U''('''x''')는 적용된 힘과 관련된 퍼텐셜 에너지라고 한다. 퍼텐셜 에너지를 갖는 힘의 예로는 중력과 용수철 힘이 있다.^[7]

힘장 '''F'''('''x''')가 주어지면, 기울기 정리를 이용한 일 적분의 계산을 통해 위치 에너지와 관련된 스칼라 함수를 구할 수 있다.

힘장에 의해 물체에 가해지는 일률은 작용점의 속도 '''v''' 방향으로의 일 또는 퍼텐셜의 기울기에서 얻어지며, 즉

: $P(t) = -{\nabla U} \cdot \mathbf{v} = \mathbf{F}\cdot\mathbf{v}.$ 이다.

퍼텐셜 함수로부터 계산할 수 있는 일의 예로는 중력과 용수철 힘이 있다.^[8]

5. 일과 위치 에너지

위치 에너지는 계에 저장되는 에너지로, 에너지 준위가 낮은 쪽으로 물체를 끌어당기는 힘, 즉 복원력이 작용할 때 존재한다. 예를 들어 용수철이 왼쪽으로 늘어나면 원래 형태로 돌아가려는 힘이 오른쪽으로 작용한다. 이와 유사하게, 어떤 질량이 지면에서 들어 올려질 경우 아래 방향으로 중력이 작용하여 낮은 위치가 되도록 한다.^[8] 처음 질량을 들어 올리거나 용수철을 당길 때 에너지가 필요하다. 질량을 들어 올리기 위해 가해준 에너지는 중력장 하의 그 물체의 위치에 저장된다. 용수철을 놓거나 질량을 떨어뜨렸을 때, 이 저장된 에너지는 복원력에 의해 운동 에너지로 바뀐다. 여기서 복원력은 용수철의 경우 탄성력이며, 질량의 경우 중력이다.^[8] 롤러코스터를 생각해보면, 롤러코스터가 경사를 올라갈 때 위치 에너지를 가지게 되며, 최고점에서 위치 에너지가 가장 크다. 롤러코스터가 다시 빠른 속도로 내려가면서 위치 에너지는 운동 에너지로 바뀌며, 최저점에서 운동 에너지가 가장 크다. (마찰로 손실되는 에너지를 무시하면, 운동 에너지와 위치 에너지는 에너지 보존의 법칙을 만족한다.)

좀 더 엄밀하게 말하면 위치 에너지는 상대적인 위치에 따라 물체가 가지는 에너지 간의 차이를 의미하며, 그렇지 않은 경우는 기준점이나 기준면을 정해서 사용한다.

위치 에너지에는 다양한 종류가 있으며, 각각의 위치 에너지에는 각각의 힘이 대응한다. 예를 들면, 탄성력에 대해 한 일은 탄성 위치 에너지이며, 중력의 경우 중력 위치 에너지, 전기력의 경우는 전기 위치 에너지, 바리온 입자가 강한 핵력이나 약한 핵력에 대해 한 일은 핵 위치 에너지, 분자력에 대한 일은 분자 간 위치 에너지라고 한다. 또한 화석 연료 따위에 저장된 에너지를 일컫는 화학 위치 에너지는 분자 내부의 재배열 과정 중에 전기력에 대해 한 일이 된다.

위치 에너지에서 유도할 수 있는 힘은 보존력이라고도 부른다. 보존력이 한 일은 다음과 같이 나타낼 수 있다.

: $\,W = -\Delta U$

이 때 $\Delta U$ 는 힘에 의한 위치 에너지의 변화를 의미한다. 마이너스 기호는 역장과 반대 방향으로 행해진 일이 위치 에너지를 증가시켰음을 의미하며, 역장에 의한 일은 위치 에너지를 감소시킨다. 일반적으로 위치 에너지를 나타내는 기호로 ''U'', ''V'', 그리고 ''E_p''를 사용한다.

힘이 움직이는 물체에 작용할 때, 일의 적분이 경로에 무관하다면 그 일은 퍼텐셜 에너지의 변화를 나타낸다. 힘 '''F'''와 그 작용점의 속도 '''v'''의 스칼라 곱은 특정 시간에 시스템에 입력되는 일률을 정의한다. 이 일률을 작용점의 궤적 ''d''='''x'''(t)에 대해 적분하면 힘에 의해 시스템에 입력된 일을 정의한다.

적용된 힘에 대한 일이 경로에 무관하다면, 힘이 한 일은 작용점의 궤적의 시작과 끝에서 평가된다. 즉, "퍼텐셜"이라고 하는 함수 ''U''('''x''')가 있으며, 이 함수는 두 점 '''x'''_A와 '''x'''_B에서 평가하여 이 두 점 사이의 임의의 궤적에 대한 일을 얻을 수 있다. 양의 일이 퍼텐셜의 감소가 되도록 이 함수를 음수 부호로 정의하는 것이 관례이며, 다음과 같다.

: $W =\int_{C} \mathbf{F} \cdot d\mathbf{x} = U(\mathbf{x}_\text{A})-U(\mathbf{x}_\text{B})$

여기서 ''C''는 A에서 B로 이동하는 궤적이다. 일이 경로에 무관하기 때문에, 이 식은 A에서 B로 가는 임의의 궤적 ''C''에 대해 성립한다.

함수 ''U''('''x''')는 적용된 힘과 관련된 퍼텐셜 에너지라고 한다. 퍼텐셜 에너지를 갖는 힘의 예로는 중력과 용수철 힘이 있다.

예를 들어, 손으로 공을 들어 올려서 천천히 놓는 경우를 생각해 보자. 공은 중력에 따라 아래로 떨어진다.

여기서 이 공이 가지는 에너지에 주목하자. 공을 들어 올렸을 때, 그 공은 '''위치 에너지'''를 얻었다고 생각한다. 얻은 에너지의 크기는 공을 들어 올리는 데 필요한 에너지와 같다. 그리고 공을 지탱하던 손이 놓인 순간, 위치 에너지는 운동 에너지로 변하기 시작한다. 운동 에너지란 물체가 움직이고 있을 때 가지는 에너지이다. 공이 떨어짐에 따라 위치 에너지는 감소하고, 대신 운동 에너지는 증가한다. 위치 에너지와 운동 에너지의 합, 즉 물체가 가지는 모든 에너지를 역학적 에너지라고 한다.

위 그림은 낙하하는 물체의 에너지 변화를 나타낸다. ''h''는 물체의 높이, ''t''는 시간, ''E_pot''는 위치 에너지, ''E_kin''는 운동 에너지, ''E_tot''는 역학적 에너지이다. 물체가 낙하함에 따라 위치 에너지(노란 부분)는 감소하고, 운동 에너지(파란 부분)는 증가한다.

여기서 중요한 것은 공이 낙하하는 동안 역학적 에너지는 항상 일정하게 변하지 않는다는 것이다. 물체가 움직일 때는 에너지의 종류는 변하지만 그 총량은 증가하거나 감소하지 않는다. 이 법칙을 역학적 에너지 보존 법칙이라고 한다. 운동 에너지를 ''K'', 위치 에너지를 ''U'', 역학적 에너지를 ''E''라고 하면, ''K＋U＝E''로 나타낼 수 있다. 이것은 뉴턴 역학 3법칙으로부터 유도할 수 있다.

6. 힘점에 의한 운동 (천문학 및 미시물리학)

천문학이나 미시물리학에서는 불특정 힘원점에 대해 에너지를 기술해야 한다. 이때는 위치 에너지의 기준을 정할 수가 없기 때문에 무한 원점을 위치 에너지 기준면으로 삼는다.

참조

_[1] 서적 Textbook of Engineering Physics, Part 1 PHI Learning Pvt. Ltd.
_[2] 서적 Physics of the Human Body https://archive.org/[...] JHU Press 2010
_[3] 서적 Chemistry The Central Science https://archive.org/[...] Pearson Education, Inc.
_[4] 서적 The Science of Energy – a Cultural History of Energy Physics in Victorian Britain The University of Chicago Press 1998
_[5] 간행물 On the general law of the transformation of energy
_[6] 학술지 What is potential energy? https://iopscience.i[...] 2023-02-15
_[7] 서적 Classical Mechanics https://books.google[...] University Science Books 2005
_[8] 서적 Kinematics and dynamics of planar machinery https://books.google[...] Prentice-Hall 1979
_[9] 웹사이트 The Feynman Lectures on Physics Vol. I Ch. 13: Work and Potential Energy (A) https://feynmanlectu[...]
_[10] 웹사이트 Hyperphysics – Gravitational Potential Energy http://hyperphysics.[...]
_[11] 서적 The Inflationary Universe Perseus Books 1997
_[12] 뉴스 Energy storage – Packing some power http://www.economist[...] 2011-03-03
_[13] 웹사이트 Pumped storage in Switzerland – an outlook beyond 2000 http://www.stucky.ch[...] 2012-02-13
_[14] 웹사이트 Pumped Hydroelectric Energy Storage and Spatial Diversity of Wind Resources as Methods of Improving Utilization of Renewable Energy Sources http://www.colorado.[...] 2012-02-12
_[15] 웹사이트 Pumped Hydroelectric Storage http://www.duke.edu/[...] 2012-02-12
_[16] 웹사이트 Energy Storage http://www.heco.com/[...] 2012-02-13
_[17] 뉴스 Packing Some Power: Energy Technology: Better ways of storing energy are needed if electricity systems are to become cleaner and more efficient http://www.economist[...] 2012-03-03
_[18] 뉴스 Ski Lifts Help Open $25 Billion Market for Storing Power https://www.bloomber[...] 2012-09-06
_[19] 웹사이트 Storing Energy on Rail Tracks http://www.leonardo-[...] 2013-10-30
_[20] 서적 Introduction to the theory of ferromagnetism https://archive.org/[...] Clarendon Pr. 1996
_[21] 서적 Classical electrodynamics https://archive.org/[...] Wiley 1975
_[22] 서적 Rising Force: The Magic of Magnetic Levitation President and Fellows of Harvard College 2011
_[23] 서적 Comprehensive Physics XII Laxmi Publications 2004
_[24] 서적 The Science of Energy - a Cultural History of Energy Physics in Victorian Britain The University of Chicago Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com